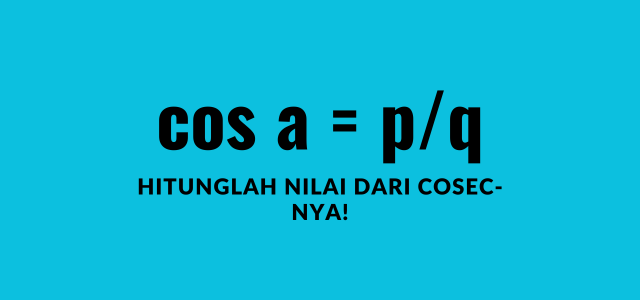Membuktikan persamaan di atas bisa dengan menggunakan salah satu sifat trigonometri. Sifat ini mesti dihafalkan karena sangat berguna untuk beberapa soal sudut seperti ini.
Gunakan sesuai rumus.
Untuk cara yang kedua kita langsung menggunakan rumus jadi yang sudah diperoleh dari pembuktian di atas.
Kita gunakan rumus aslinya.
Untuk cara kedua langsung menggunakan hasil pembuktian seperti di bawah.
Sifat yang membantu
Untuk membuktikan persamaan ini, kita hanya membutuhkan satu sifat saja. Sifat ini sudah cukup memberikan jawaban yang tepat.
Ini sifatnya :
- sin(p-q) = sin p×cos q - cos p×sin q
Nah...
Itulah sifat yang akan digunakan.
Membuktikan persamaannya
Sekarang kita terapkan ke persamaan yang ditanya.
Apakah sin(90-a) = cos a?
Ayo kita kerjakan!!
sin(90-a) = sin90×cos a - cos90×sin a
- Perhatikan lagi sifat yang sudah diberikan di atas
sin (p-q) = sin p×cos q - cos p×sin q - sin(90-a)
maka p = 90
q = a
Selanjutnya...
- Ingat nilai sin dan cos dari sudut 90
- sin 90 = 1
- cos 90 = 0
- Ini harus dihafalkan ya
sin(90-a) = 1×cos a - 0×sin a
sin(90-a) = cos a - 0
sin(90-a) = cos a
Jadi...sin(90-a) = cos a...(TERBUKTI!!)
Seperti itulah prosesnya ya.
Contoh soal
Sesudah membuktikan sifat di atas, sekarang kita coba dengan contoh soalnya. Di sini akan dibahas dengan dua cara.
Soal :
1. Hitunglah hasil dari sin(90-15)!
1. Hitunglah hasil dari sin(90-15)!
Kita mulai dari cara pertama.
Cara pertama
sin(p-q) = sin p×cos q - cos p×sin q
sin(90-15)
- Berarti p = 90
- q = 15
sin(90-15) = sin 90×cos 15 - cos 90×sin 15
- sin 90 = 1
- cos 90 = 0
sin(90-15) = 1×cos 15 - 0×sin 15
sin(90-15) = cos 15 - 0
sin(90-15) = cos 15
Jadi, inilah jawabannya.
Cara pertama masih menggunakan sifat aslinya agar anda paham bagaimana proses pengerjaannya.
Cara kedua
Hasil pembuktian :
sin(90-a) = cos a
Soalnya adalah sin(90-15), artinya
- a = 15
- Sekarang ganti a dengan 15
sin(90-a) = cos a
sin(90-15) = cos 15
Nah...
Itulah hasil jika menggunakan rumus pembuktian yang sudah kita dapatkan.
Bagaimana, sudah dimengerti kan??
Untuk cos 15 dibiarkan saja ya, karena hasilnya ada banyak koma. Dan 15 juga bukan tergolong sudut istimewa.
Biarkan saja seperti itu.
Soal :
2. Berapakah nilai dari sin(90-20)!
2. Berapakah nilai dari sin(90-20)!
Soal ini juga diselesaikan dengan dua cara, sama seperti soal pertama.
Cara pertama
sin(p-q) = sin p×cos q - cos p×sin q
sin(90-20)
- Artinya, p = 90
- q = 20
sin(90-20) = sin 90×cos 20 - cos 90×sin 20
- sin 90 = 1
- cos 90 = 0
sin(90-20) = 1×cos 20 - 0×sin 20
sin(90-20) = cos 20 - 0
sin(90-20) = cos 20
Itulah jawaban yang dimaksud.
Biarkan saja hasilnya dalam bentuk cos 20.
Cara kedua
sin(90-a) = cos a
Soalnya adalah sin(90-20), artinya
- a = 20
- Langsung ganti a dengan 20
sin(90-a) = cos a
sin(90-20) = cos 20
Jawabannya sama, yaitu cos 20.
Fakta menarik lain
Mari kita pakai soal pertama.
sin(90-15) = cos 15
- Sekarang kurangkan 90 dengan 15
- Hasilnya 75
sin 75 = cos 15
Nah...
Kita dapatkan data menarik kalau sin 75 itu hasilnya sama dengan cos 15.
Bisa dibuktikan dengan kalkulator.
Bisa dilihat pada gambar di atas.
sin 75 dan cos 15 memberikan hasil yang sama, yaitu 0,9659.
Soal nomer dua juga sama.
sin(90-20) = cos 20
- kurangkan 90 dengan 20 menjadi 70
sin 70 = cos 20
Untuk membuktikan silahkan gunakan kalkulator ya!!
Baca juga ya :